Descomplicando a Busca Binária
Recentemente, tenho dedicado uma parte significativa dos meus estudos à compreensão de estruturas de dados e algoritmos. Apesar de ter passado a maior parte da minha carreira como desenvolvedor front-end, focado principalmente em design e interface do usuário, sempre nutri uma curiosidade intrínseca pela manipulação eficiente de dados.
Neste artigo, busco explicar os conceitos básicos de uma busca binária, suas aplicações e, por fim, apresentar um modelo prático em JavaScript.
O custo de uma busca
Quando começamos a lidar com conjuntos de dados em programação, especialmente através de listas, é comum não nos preocuparmos muito com o desempenho. Afinal, os principais objetivos ao optarmos pelo uso de uma lista são organização, consulta e remoção dos dados.
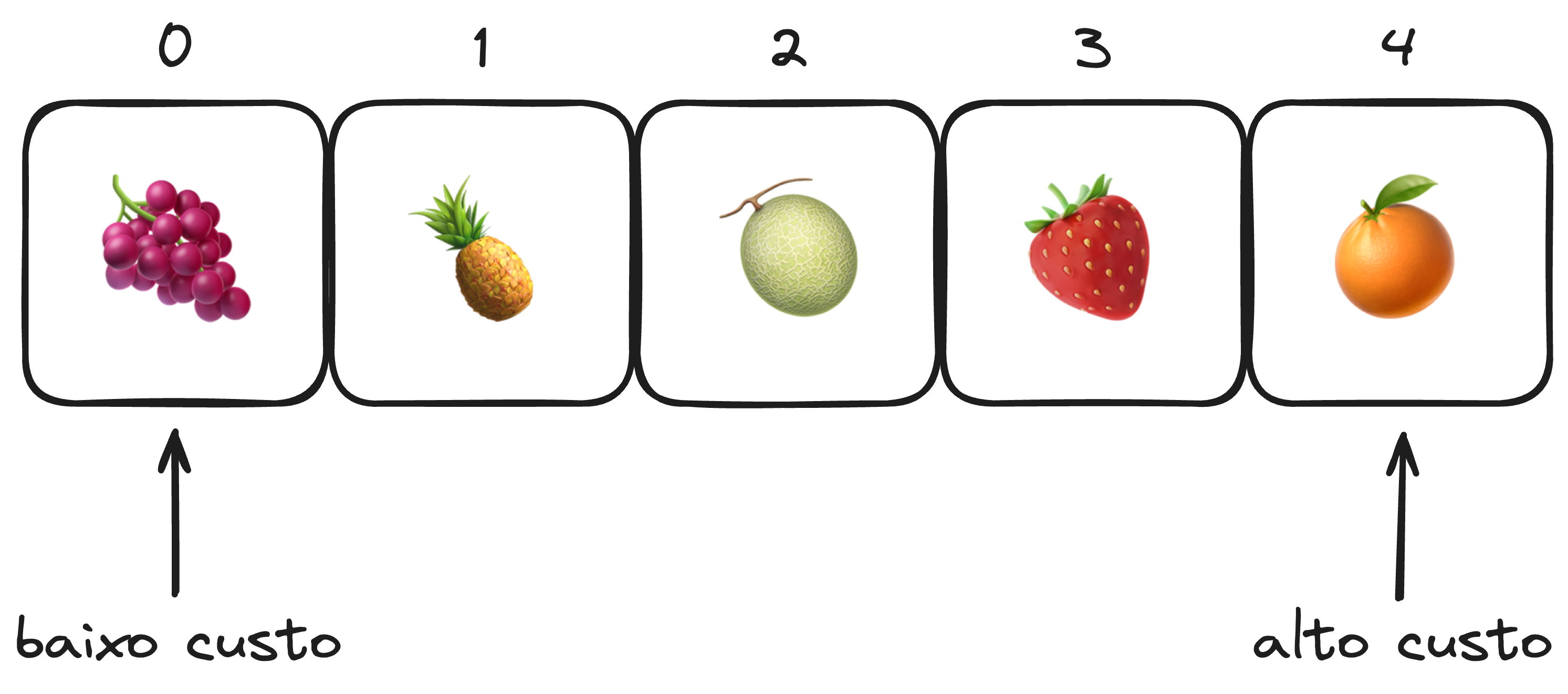
Tomemos como exemplo a lista abaixo, onde temos uma estrutura armazenando o nome de 5 frutas. Nesse contexto, é relativamente simples aplicar um laço de repetição para encontrar o índice de uma fruta pelo nome. Do ponto de vista computacional, o custo para encontrar qualquer fruta nessa lista seria mínimo.
const frutas = ['Uva', 'Abacaxi', 'Melão', 'Morango', 'Laranja'];
function buscarIndiceDaFrutaPeloNome(frutas = [], nome) {
for (let i = 0; i < frutas.length; i++) {
console.log(`Operação: ${i + 1}`);
if (nome === frutas[i]) {
return i;
}
}
}
const indiceUva = buscarIndiceDaFrutaPeloNome(frutas, 'Uva');
Entretanto, é importante questionar se o custo operacional para retornar o índice da fruta Uva é o mesmo para Laranja. A resposta é não. Embora neste exemplo os índices sejam apresentados quase que instantaneamente para cada item da lista, o custo operacional tende a aumentar à medida que o item desejado está mais próximo do fim da lista. Portanto, encontrar o índice de Laranja é mais demorado para o computador do que encontrar o índice de Uva.

Isso se torna evidente quando contamos as operações executadas pela função buscarIndiceDaFrutaPeloNome na tentativa de encontrar o índice correspondente à fruta desejada.
Encontrar o índice da Uva:
| Operação | Execução |
|---|---|
| 1 | 👉 Verifica se Uva é igual a Uva |
Encontrar o índice da Laranja:
| Operação | Execução |
|---|---|
| 1 | Verifica se Uva é igual a Laranja |
| 2 | Verifica se Abacaxi é igual a Laranja |
| 3 | Verifica se Melão é igual a Laranja |
| 4 | Verifica se Morango é igual a Laranja |
| 5 | 👉 Verifica se Laranja é igual a Laranja |
Podemos observar que encontrar o índice da Uva requer apenas uma operação, já que este é o primeiro elemento da lista. Portanto, podemos dizer que o custo dessa operação é $ O(1) $ na notação Big O.
Por outro lado, encontrar o índice da Laranja requer 5 operações, já que este é o último elemento da lista. Assim, podemos representar o custo dessa operação como $ O(n) $, onde $ n $ é o número de elementos na lista.
Claro, em um contexto com apenas algumas operações, como o exemplo das frutas, o custo computacional de cinco operações é praticamente negligenciável para um computador. No entanto, ao considerarmos um sistema com uma lista significativamente maior, como, por exemplo, 1.500 frutas, a história muda.
Se imaginarmos que cada operação leva 0.5 segundos para ser concluída, encontrar o índice da última fruta na lista levaria aproximadamente 750 segundos. Isso se traduz em cerca de 12 minutos e meio de tempo de resposta do sistema. Portanto, embora o custo de cada operação seja pequeno, quando multiplicado pelo número total de operações necessárias, o tempo total de processamento pode se tornar substancial.
Diante desse cenário, surge a pergunta crucial: como podemos otimizar essa busca?
Ordenação é o segredo
Geralmente, ao procurarmos um documento em uma pasta ou um contato em uma agenda, observamos que esses itens estão ordenados para facilitar sua localização. Na programação, não é diferente.
Imagine uma lista com 7 números:
const numeros = [10, 23, 53, 87, 24, 2, 61]
Baseando-nos no exemplo anterior das frutas, uma busca linear (verificando item a item) para encontrar o índice do número 2 custaria um total de 6 operações computacionais. E se ordenarmos essa lista?
const numeros = [2, 10, 23, 24, 53, 61, 87]
Após a ordenação, precisaríamos de apenas 1 operação para o sistema encontrar o índice do número 2. Mas será que essa redução no custo operacional se aplica a todos os itens?
Vamos analisar o cenário do número 61. Na busca linear, precisaríamos de 6 operações para encontrar seu índice, mesmo com a lista ordenada. No entanto, ao invés de começarmos a busca pelo começo, por que não começar pelo meio?
Para determinar o meio da lista, devemos considerar onde ela começa e onde termina. Com essas informações, podemos fazer um simples cálculo somando o início e o fim e dividindo por 2 para encontrar a metade exata. Assim, temos:
const baixo = 0
const alto = numeros.length - 1
const meio = Math.floor((baixo + alto) / 2)
Onde na lista de números o meio será o índice 3, correspondente ao valor 24.
Dessa maneira, se considerarmos o índice 3 como ponto de partida para a lista, podemos iniciar nossa busca a partir desse elemento, uma vez que os valores estão ordenados:
| Operação | Execução |
|---|---|
| 1 | Verifica se 24 é igual a 61 |
| 2 | Reduz a lista pela metade, agora o meio é 61 |
| 3 | Verifica se 61 é igual a 61 |
Começando a busca pelo meio da lista, reduzimos o número de operações de 6 para 3 até encontrarmos o número 61. Esse é o primeiro exemplo prático de como uma busca binária funciona.
Com a pesquisa binária, você seleciona o número intermediário de uma lista e elimina a metade dos números restantes a cada operação.

Isso faz com que você não precise ler todos os elementos da lista para encontrar o elemento desejado, uma vez que, a cada operação, a lista é reduzida pela metade. Analisando os valores lidos da lista a cada operação binária, temos o seguinte comportamento:
| Operação | Execução |
|---|---|
| 1 | [2, 10, 23, 24, 53, 61, 87] (verifica o meio 24) |
| 2 | [53, 61, 87] (divide a lista) |
| 3 | 👉 [53, 61, 87] (verifica o meio 61) |
Novamente, se considerarmos apenas uma lista com 7 elementos, talvez a diferença entre realizar 6 ou 3 operações em uma busca não pareça tão significativa para o sistema. No entanto, se ampliarmos o escopo para uma lista ordenada com 100 números, a busca linear exigiria 100 operações para encontrar o último elemento. Por outro lado, a busca binária levaria apenas 7 operações!
Enquanto a busca linear opera na notação $ O(n) $, a busca binária demonstra alto desempenho, reduzindo pela metade o número de leituras a cada operação. Isso se traduz em:
$$ O(\log n) $$
Um belo algoritmo para buscar
Dado que em cada operação dividimos a lista e verificamos se o elemento no meio é o valor desejado, podemos simplesmente aplicar essa lógica em um loop de repetição para obter nosso algoritmo:
function pesquisaBinaria(lista, item) {
let baixo = 0;
let alto = lista.length - 1;
let meio, chute;
while (baixo <= alto) {
meio = Math.floor((baixo + alto) / 2);
chute = lista[meio];
if (chute === item) {
return meio; // Retorna o índice se o item for encontrado
}
if (chute > item) {
alto = meio - 1; // Descarta a metade superior da lista
} else {
baixo = meio + 1; // Descarta a metade inferior da lista
}
}
return -1; // Retorna -1 se o item não for encontrado na lista
}
Dessa forma, ao fornecermos uma lista ordenada para a função pesquisaBinaria e especificarmos o valor desejado, receberemos o índice correspondente como retorno:
const indice = pesquisaBinaria([1,3,5,7,9], 5)
console.log(indice) // 2
Por fim, vale ressaltar alguns pontos importantes sobre a implementação da busca binária:
- A busca binária requer que a lista esteja previamente ordenada.
- Em cada operação, a busca binária encontra a metade da lista e verifica se este é o elemento desejado.
- Ao contrário da busca linear, a busca binária opera em tempo logarítmico.
- Quanto mais longa a lista, mais evidente se torna a vantagem da busca binária em relação à busca linear.
